Lissajous Curves
The mathematical understanding of the ABC logo.
Lissajous curves are most likely one of simplest, most practical and coolest looking curves to come out of mathematics. They were intently studied by a Frenchman known as Jules Antoine Lissajous, using combinations of tuning forks and mirrors but have served a much more practical purpose since. Often electronics technicians and engineers would use the properties of Lissajous curves as a basis for tuning equipment. If an input is set at 1kHz for example and a figure of 8 is shown on an oscilloscope or display, the technician can deduce that the secondary signal he is measuring is 2kHz purely by sight or on a logarithmic scale 10kHz. By memorising the look of important harmonics of the signals it is a very quick way or working out whether you are in the correct ballpark without advanced equipment.
Mathematically these curves are described using a set of parametric equations:
\[\begin{aligned} x(t)&=A\cos(\omega_1 t + \delta_1)\\ y(t)&=B\cos(\omega_2 t + \delta_2) \end{aligned}\]For the below there is only 1 delta on the y component, the amplitudes \(A\) and \(B\) are set to 1 and are names according to \(\omega_1\)-\(\omega_2\). Some visualisations of what this actually looks like:
The 1-1 Lissajous:
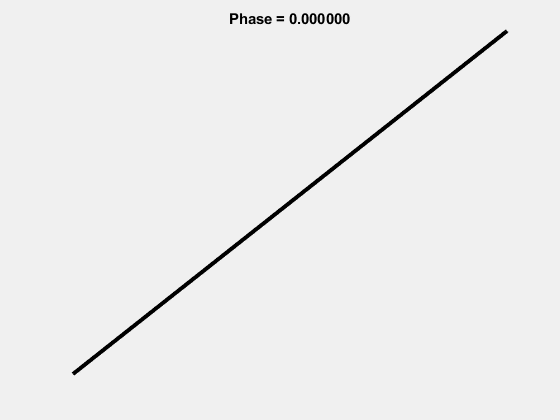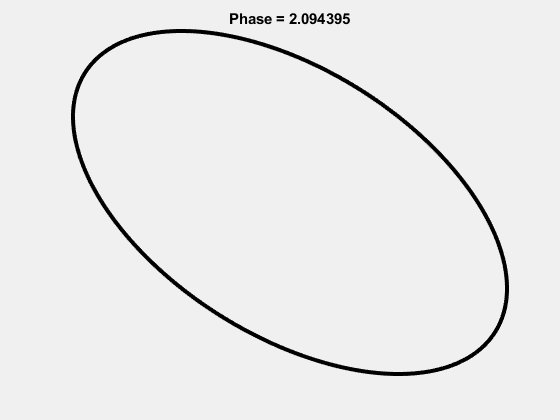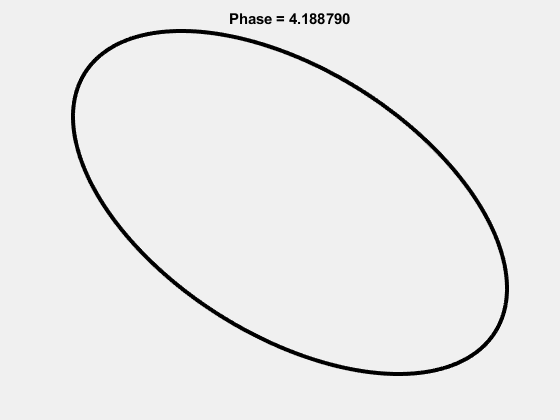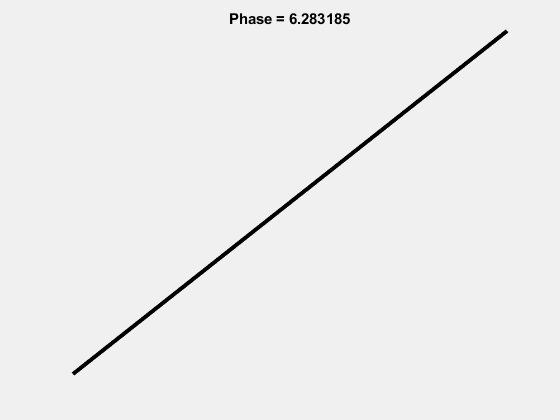
The 2-5 Lissajous:
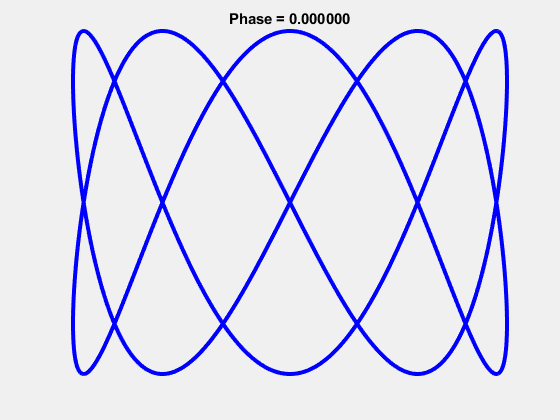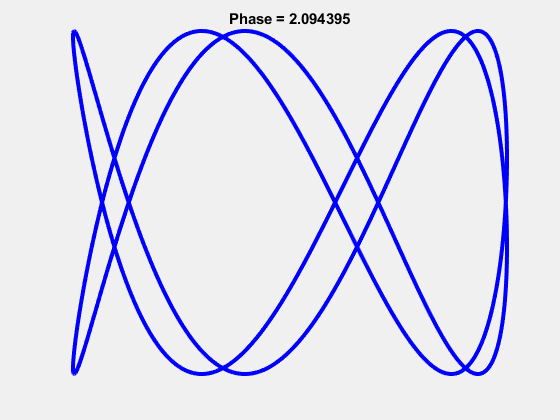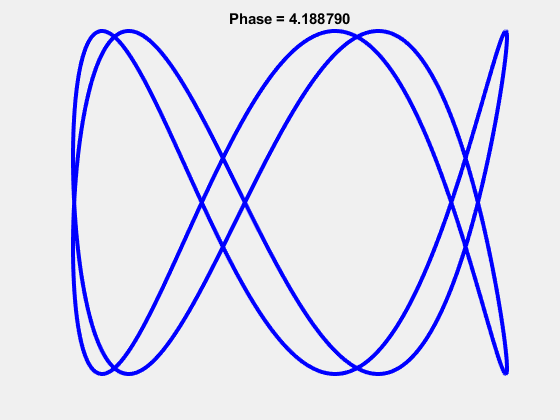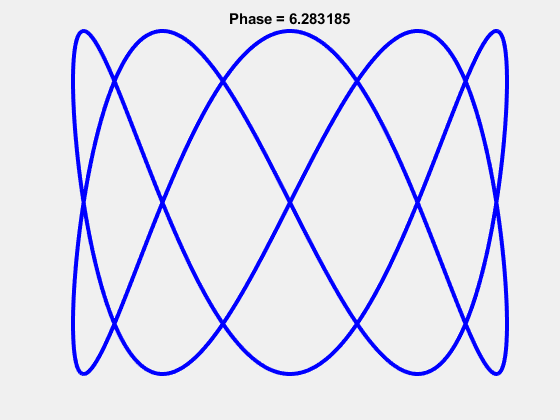
The 3-7 Lissajous:
The ABC Logo
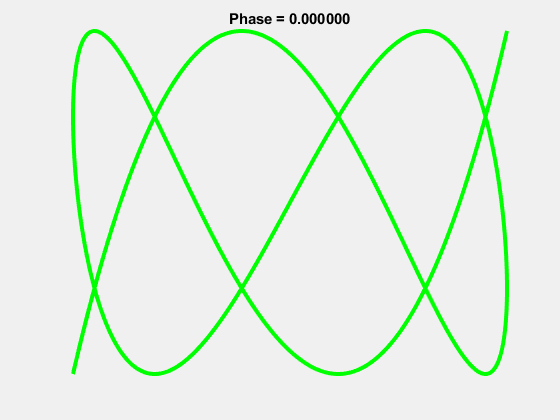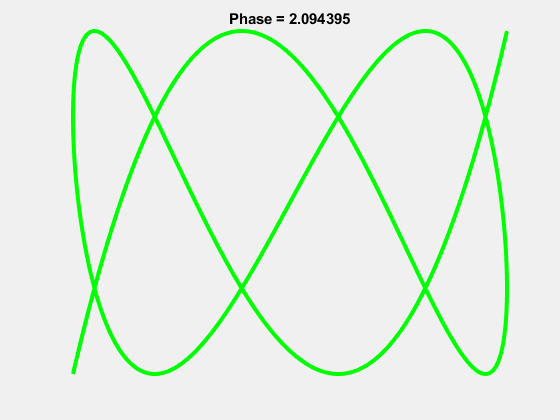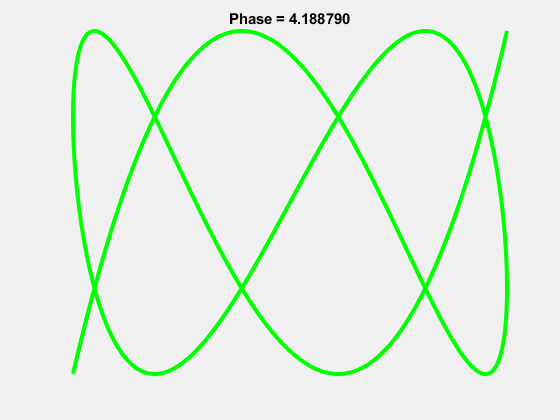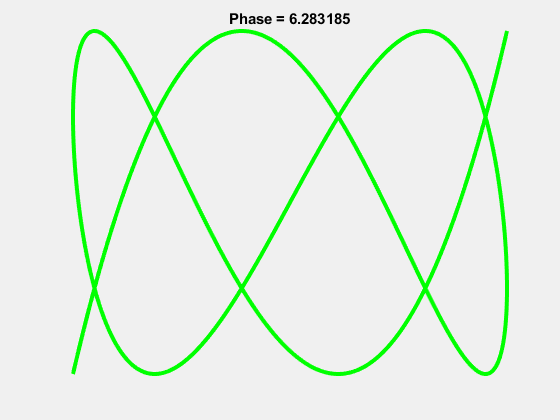
Yes it turns out the beloved “worm” logo of Aunty is in fact a Lissajous curve, the 1-3 Lissajous to be exact.
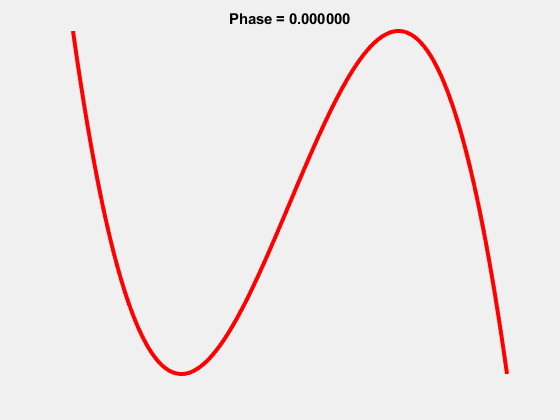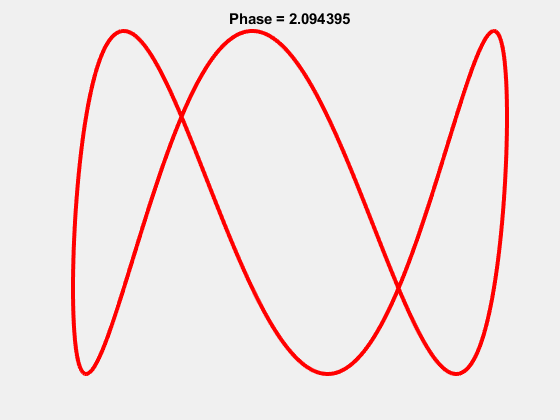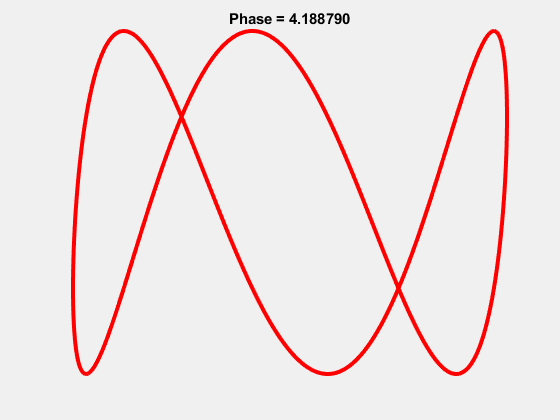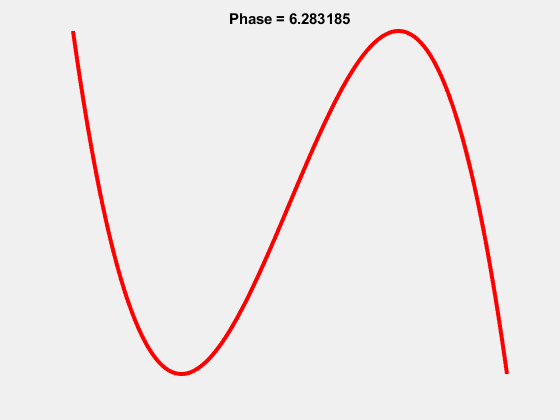
And the “worm” actually occurs properly at a phase shift of \(\pi/2\):
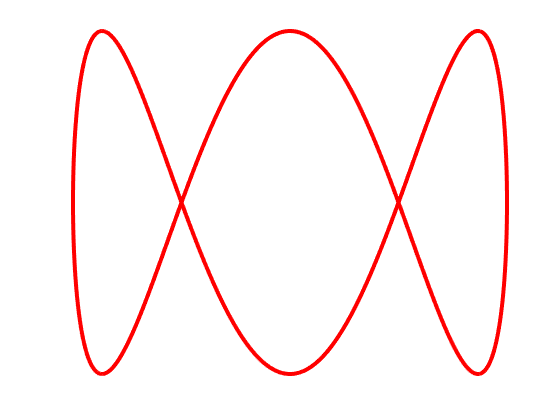
It’s been said that the ABC wanted their logo to be the 1-2 Lissajous which resembled \(\infty\) with each loop representing their two branches: TV and Radio. This was in use however by the University of the Air as a logo, so they settled on the 1-3. As the ABC now has 3 branches: TV, Radio and Online, it seems fitting that the logo now reaches the intended significance. They must have known something!